AXEC: Knowledge only

AXECwiki

Debunking squared

"What enabled me to break away from that delusional analysis was what the Australians call ‘a good bullshit detector.’" (Keen, 2011, p. 268)

Steve Keen has, with the help of his fabulous detector, divined a lot of analytical blunder and debunked a good part of standard economics. Rightly so, because to clear the heads is the indispensable preparatory task of heterodox economics. However, Keen has left standing the theory of profit. This is unfortunate because
the theory of profit is the pivot of all of theoretical economics. What deserves the first and foremost attention is in any case the factual relation of profit and income.

Steve Keen has stated the definition of income in two prominent places as: “Total income = Wages plus Profits” (2011, p. 366) and “. . . national income resolves
itself into wages and profits” (2010, p. 12). This, of course, is what we have heard often from middle-of-the-road economists but also from Keynes (1973, p. 23).
This definition seems to be plain common sense, yet, like most common sense since Aristotle, it is demonstrably false (2012). Therefore, what is required for the
advancement of Heterodoxy is to debunk the naive definition of total income.

This is done in the following with a straightforward graphical demonstration. For the rigorous formal underpinning and the full implications see (2013b, 2011). Figure 1 shows the simplest possible configuration of the elementary production-consumption economy.

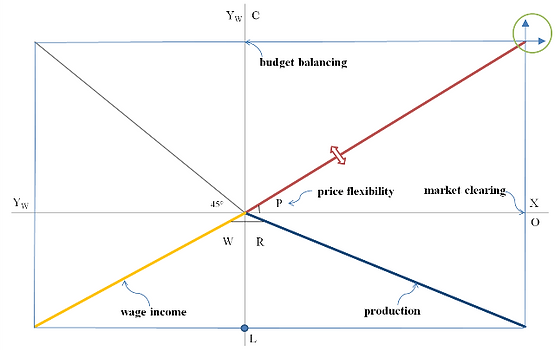
Figure 1: The price in period t=1 is objectively determined by the conditions of market clearing and budget balancing. Legend: P price, L employment, W wage rate, YW wage income, C consumption expenditure, R productivity, O output, X quantity bought

At any given level of employment L, the wage income YW that is generated in the consolidated business sector follows by multiplication with the wage rate W. On the real side output follows by multiplication with the productivity. Finally, the price follows as the dependent variable under the conditions of budget balancing, i.e. C=YW and market clearing, i.e. X=O. Note that the ray in the southeastern quadrant is not a linear production function; the ray tracks any underlying production function. The same holds for the distribution of wage incomes in the southwestern quadrant. All these details are not needed at the moment.

It can be directly read off from the 4-quadrant scheme that the real wage W/P is always equal to the productivity R, that is, labor gets the whole product, no matter what. If the wage rate is lowered, the market clearing price falls. If the number of working hours is increased the price remains constant, provided productivity does not change. If productivity decreases the price rises. In any case, labor gets the whole product and profit is zero, or in Walras’s terms, there is ‘ni bénéfice ni perte’, neither profit nor loss. So far, all are agreed:

"The consensus to date has been that it is mathematically impossible for capitalists in the aggregate to make profits." (Keen, 2010, p. 2)

There is also explicit assent from economics methodology.

". . . since it is impossible to have an economy where everyone is making profits. Aggregate profit for an entire (closed) economy must be zero,
hence if any firm is making profits, some other firm must be making losses." (Boland, 1992, p. 80)

The weak spot in the otherwise impeccable zero-profit argument is that aggregate profit has been greater than zero for most of the time in most of the known market economies up to the present. Hence Figure 1 is the first but not the last word in the theory of profit.

The crucial point is this: there exists no such thing as an immutable law of budget balancing in the same period. Just the contrary. Logically, we have three possible cases in the next period: C2<YW2, C2=YW2, C2>YW2. The first case means loss, the second zero profit, and the third profit. Figure 2 shows an example of the third case which has, compared to the others, the best evolutionary prospects in the real world.

Figure 2: Monetary profit in period t=2 is objectively determined by the difference between consumption expenditure and wage income under the condition of market clearing, irrespective of what the agents optimize

In the elementary production-consumption economy, profit can at first only be greater than zero if consumption expenditures are greater than wage income. This configuration has historically been realized in various ways, the ordinary way is that the household sector takes up credit from the banking industry (for details see 2013, Sec. 18). One pertinent example is the purchase of long-lived consumption goods like cars or homes on credit. The relation between credit expansion of the household sector as a whole and profit for the business sector as a whole is measurable in principle (Keen, 2011, pp. 337-353). The only open question is how long can Figure 2 be reproduced? After all, credit has to be redeemed someday. This eventuality is not at issue here (see 2013a).

In the case of Figure 2 monetary profit is given as Q2≡C2-YW2 in the northeastern quadrant. Profit takes the form of money in the bank and remains in the business sector in the period under consideration, i.e. profit is retained (this incidentally answers the old chestnut M–C–M+, see Keen, 2011, p. 217). Due to the higher market clearing price the real wage is now lower than the productivity.

In the next period, profit is distributed and the household sector’s total income is accordingly: Y3=YW3+YD3. If profit is fully distributed we have YD3=Q2, i.e. distributed profit in period t=3 is equal to profit in period t=2. Profit in period t=3 is in the general case: Q3≡C3-YW3+YD3. This solves the long-standing profit puzzle. The Profit Law is the first of the far-reaching implications of Figure 2. Note that profit and distributed profit is not the same thing and that both are never equal in reality. Note also that the Profit Law, when augmented with investment, foreign trade, and government, is directly testable.

Resume: Total income is the sum of wage income and distributed profit and not of wage income and profit. This distinction makes all the difference between good or bad economics. Steve Keen has debunked a large part of Orthodoxy, yet with regard to the foundational concepts income and profit Heterodoxy still subscribes to the conventional error.

References
Boland, L. A. (1992). The Principles of Economics. Some Lies my Teacher Told Me. London, New York: Routledge.

Kakarot-Handtke, E. (2011). The Emergence of Profit and Interest in the Monetary Circuit. SSRN Working Paper Series, 1973952: 1–23. URL
Kakarot-Handtke, E. (2012). The Common Error of Common Sense: An Essential Rectification of the Accounting Approach. SSRN Working Paper Series, 2124415:
1–23. URL
Kakarot-Handtke, E. (2013a). Redemption and Depression. SSRN Working Paper Series, 2343561: 1–28. URL
Kakarot-Handtke, E. (2013b). Understanding Profit and the Markets: The Canonical Model. SSRN Working Paper Series, 2298974: 1–55. URL
Keen, S. (2010). Solving the Paradox of Monetary Profits. Economics E-Journal, 4(2010-31). URL
Keen, S. (2011). Debunking Economics. London, New York: Zed Books, rev. edition.
Keynes, J. M. (1973). The General Theory of Employment Interest and Money. The Collected Writings of John Maynard Keynes Vol. VII. London: Macmillan.

***

For details see Objective Principles of Economics URL